笔者在力扣算题时,遇到股票题,觉得很有意思,于是写下自己的总结
1.第一个股票问题(一次买卖)
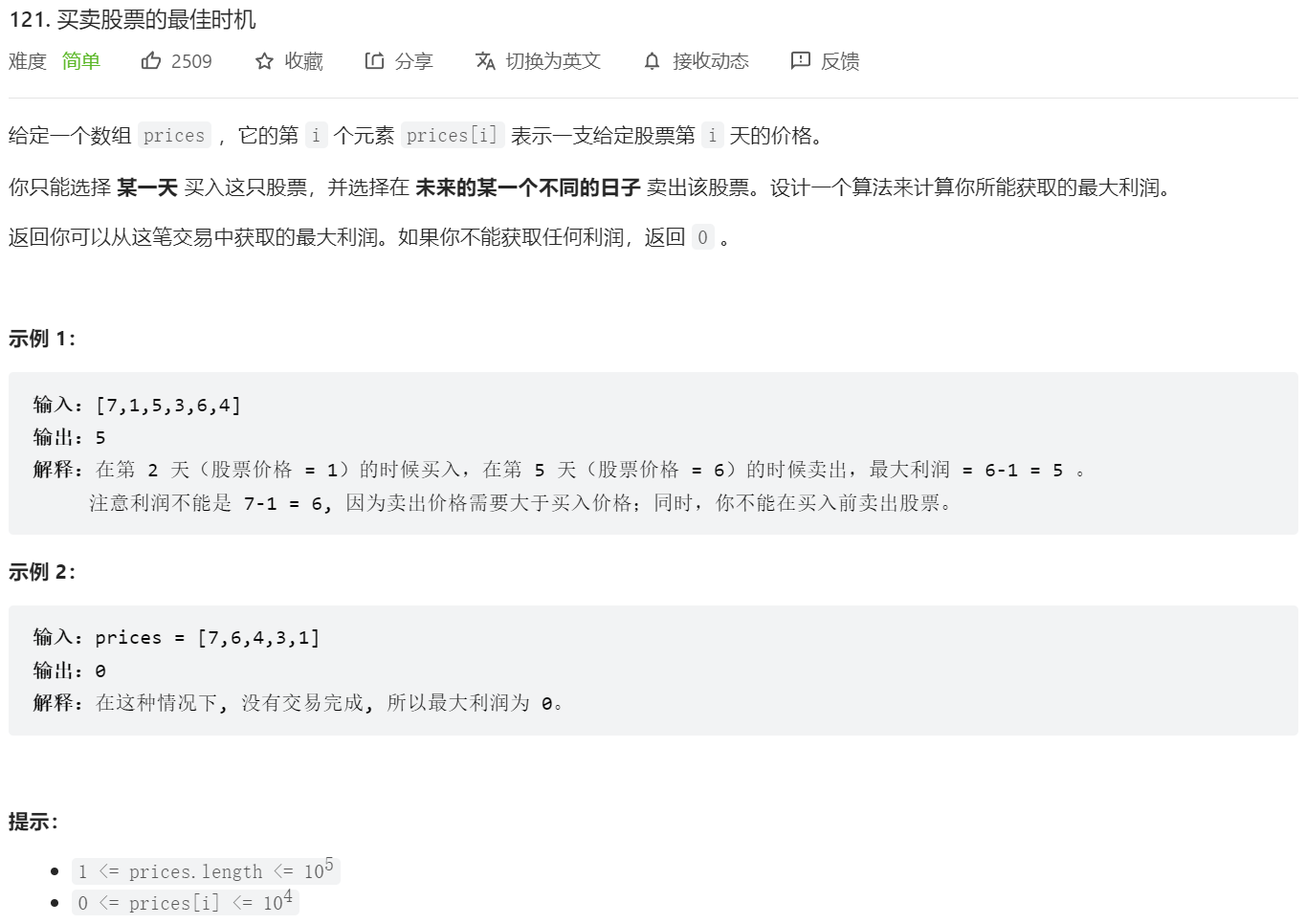
首先是最简单的题目,只有一次购买,一次卖出
思路还是挺清晰的,还是DP思想:
- 记录【今天之前买入的最小值】
- 计算【今天之前最小值买入,今天卖出的获利】,也即【今天卖出的最大获利】
- 比较【每天的最大获利】,取最大值即可
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public int maxProfit(int[] prices) {
if(prices.length <= 1)
return 0;
//初始化
int[][] dp = new int[prices.length][2];
//两个状态:手里没股票,手里有股票
dp[0][1] = -prices[0];
dp[0][0] = 0;
for(int i = 1;i < prices.length; i ++){
//手里没股票
dp[i][0] = Math.max(dp[i - 1][0],dp[i - 1][1] + prices[i]);
//手里有股票
dp[i][1] = Math.max(dp[i - 1][1],-prices[i]);
}
return dp[prices.length - 1][0];
}
}
当然因为我们只是用二维数组保存了两个状态,有股票和没股票,所以可以简化一下
class Solution {
public int maxProfit(int[] prices) {
int length = prices.length;
//两个状态:手里没股票,手里有股票
int dp0 = 0,dp1 = Integer.MIN_VALUE;
for(int i = 0;i < length; i ++){
//手里没股票
dp0 = Math.max(dp0,dp1 + prices[i]);
//手里有股票
dp1 = Math.max(dp1,-prices[i]);
}
//返回没股票的时候
return dp0;
}
}总之,没股票可以从昨天的有股票卖出,或者昨天的没股票得出(当然我们要尽量去获取最大值,毕竟利润最大),有股票可以是买今天的,或者昨天的有股票得到。
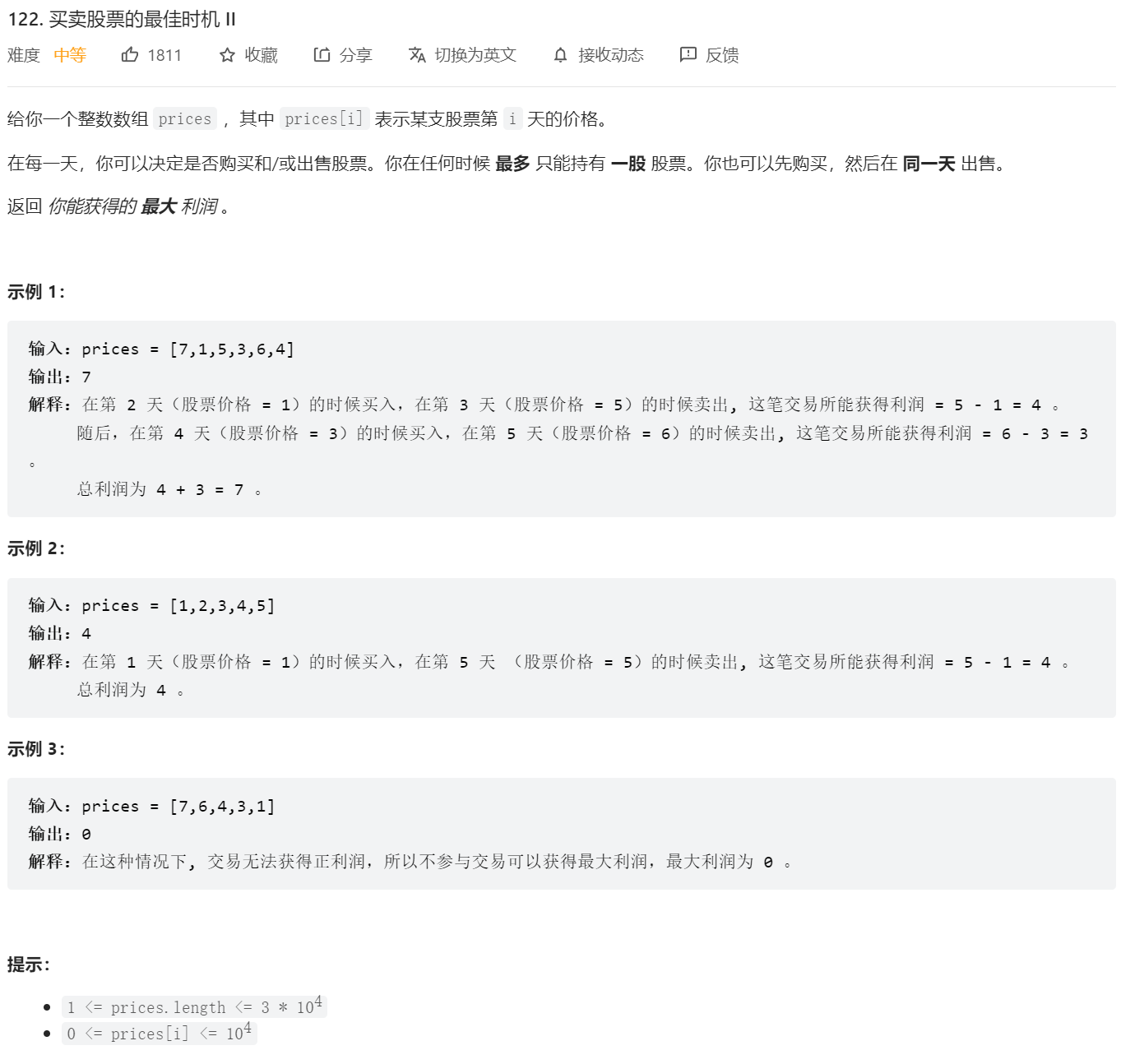
2.第二个股票问题(多次买卖)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public int maxProfit(int[] prices) {
if(prices.length <= 1)
return 0;
//初始化
int[][] dp = new int[prices.length][2];
//两个状态:手里没股票,手里有股票
dp[0][1] = -prices[0];
dp[0][0] = 0;
for(int i = 1;i < prices.length; i ++){
//手里没股票
dp[i][0] = Math.max(dp[i - 1][0],dp[i - 1][1] + prices[i]);
//手里有股票
dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][0] - prices[i]);
}
return dp[prices.length - 1][0];
}
}
注意到上面的状态转移方程中,每一天的状态只与前一天的状态有关,而与更早的状态都无关,因此我们不必存储这些无关的状态,只需要将dp[i-1][0] 和dp[i-1][1] 存放在两个变量中,通过它们计算出 dp[i][0] 和 dp[i][1] 并存回对应的变量,以便于第 i+1 天的状态转移即可。
class Solution {
public int maxProfit(int[] prices) {
if(prices.length <= 1)
return 0;
//两个状态:手里没股票,手里有股票
int dp0 = 0,dp1 = -prices[0];
for(int i = 1;i < prices.length; i ++){
//手里没股票
dp0 = Math.max(dp0,dp1 + prices[i]);
//手里有股票
dp1 = Math.max(dp1,dp0 - prices[i]);
}
//返回没股票的时候
return dp0;
}
}相比第一题,这题多了一个条件,可以多次买卖。
总之,没股票可以从昨天的有股票卖出,或者昨天的没股票得出(当然我们要尽量去获取最大值,毕竟利润最大),有股票可以是从之前没股票的状态买今天的(之前的是不能的,只能是买一次),或者昨天的有股票得到。
3.第三个股票问题(两次买卖)
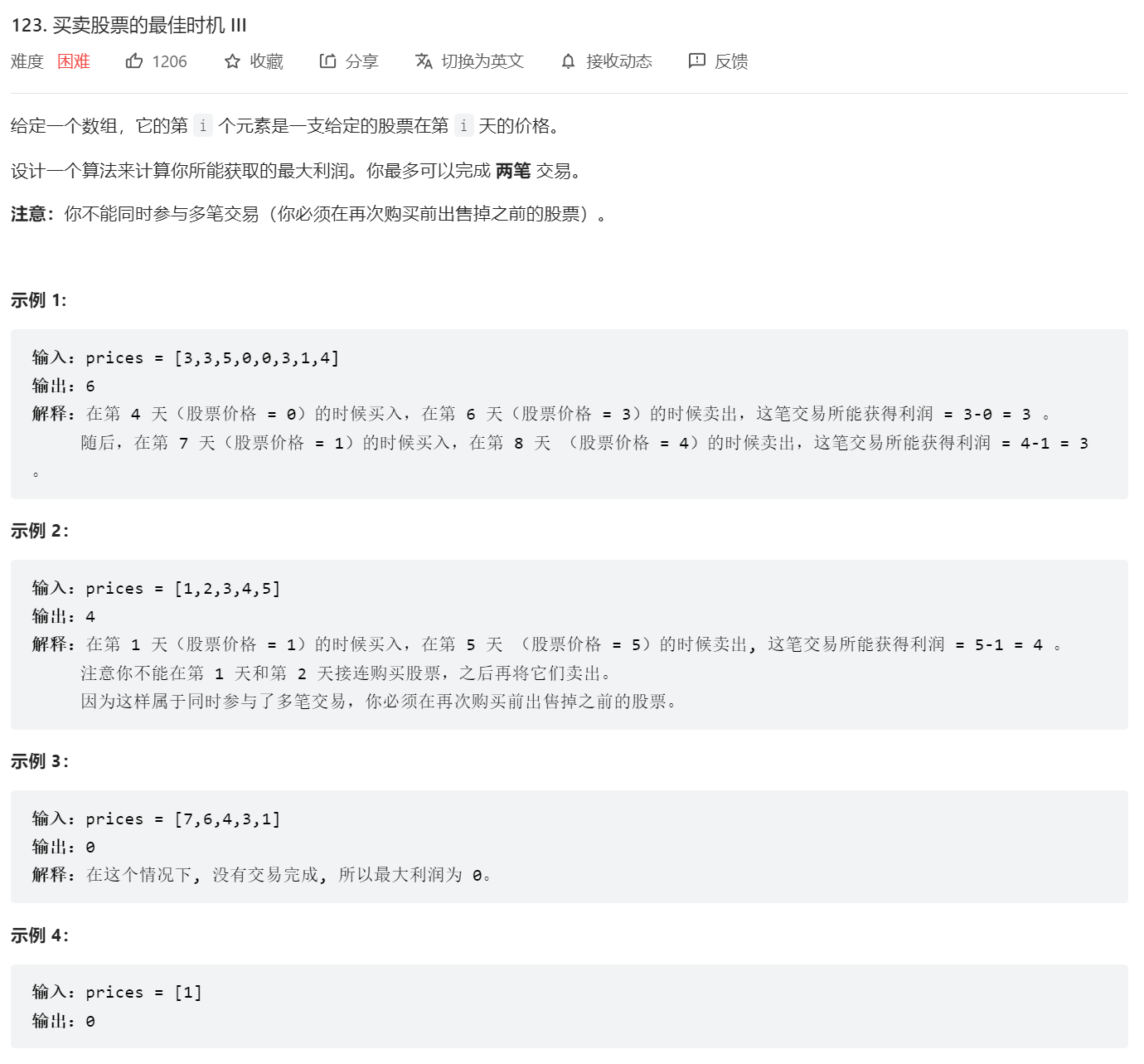
相比第二问,加了条只能买卖两次的设定,这使得我们必须要记录下数次交易中的两次最大值,所以我们必须新加状态进行购买次数的限制
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
所以定义状态转移数组dp[天数][当前是否持股][卖出的次数]
具体一天结束时的6种状态:
未持股,未卖出过股票:说明从未进行过买卖,利润为0
dp[i][0][0]=0
未持股,卖出过1次股票:可能是今天卖出,也可能是之前卖的(昨天也未持股且卖出过)
dp[i][0][1]=max(dp[i-1][1][0]+prices[i],dp[i-1][0][1])
未持股,卖出过2次股票:可能是今天卖出,也可能是之前卖的(昨天也未持股且卖出过)
dp[i][0][2]=max(dp[i-1][1][1]+prices[i],dp[i-1][0][2])
持股,未卖出过股票:可能是今天买的,也可能是之前买的(昨天也持股)
dp[i][1][0]=max(dp[i-1][0][0]-prices[i],dp[i-1][1][0])
持股,卖出过1次股票:可能是今天买的,也可能是之前买的(昨天也持股)
dp[i][1][1]=max(dp[i-1][0][1]-prices[i],dp[i-1][1][1])
持股,卖出过2次股票:最多交易2次,这种情况不存在
dp[i][1][2]=float('-inf')
class Solution {
public int maxProfitDP(int[] prices) {
if (prices == null || prices.length <= 1) return 0;
int[][][] dp = new int[prices.length][2][3];
int MIN_VALUE = Integer.MIN_VALUE / 2;//因为最小值再减去1就是最大值Integer.MIN_VALUE-1=Integer.MAX_VALUE
//初始化
dp[0][0][0] = 0;//第一天休息
dp[0][0][1] = dp[0][1][1] = MIN_VALUE;//不可能
dp[0][0][2] = dp[0][1][2] = MIN_VALUE;//不可能
dp[0][1][0] = -prices[0];//买股票
for (int i = 1; i < prices.length; i++) {
dp[i][0][0] = 0;
dp[i][0][1] = Math.max(dp[i - 1][1][0] + prices[i], dp[i - 1][0][1]);
dp[i][0][2] = Math.max(dp[i - 1][1][1] + prices[i], dp[i - 1][0][2]);
dp[i][1][0] = Math.max(dp[i - 1][0][0] - prices[i], dp[i - 1][1][0]);//持有昨天的股票,或者昨天没买,今天买了
dp[i][1][1] = Math.max(dp[i - 1][0][1] - prices[i], dp[i - 1][1][1]);
dp[i][1][2] = MIN_VALUE;
}
return Math.max(0, Math.max(dp[prices.length - 1][0][1], dp[prices.length - 1][0][2]));
}
}
大神版
class Solution {
public int maxProfit(int[] prices) {
/**
对于任意一天考虑四个变量:
fstBuy: 在该天第一次买入股票可获得的最大收益
fstSell: 在该天第一次卖出股票可获得的最大收益
secBuy: 在该天第二次买入股票可获得的最大收益
secSell: 在该天第二次卖出股票可获得的最大收益
分别对四个变量进行相应的更新, 最后secSell就是最大
收益值(secSell >= fstSell)
**/
int fstBuy = Integer.MIN_VALUE, fstSell = 0;
int secBuy = Integer.MIN_VALUE, secSell = 0;
for(int p : prices) {
//状态转移
fstBuy = Math.max(fstBuy, -p);
fstSell = Math.max(fstSell, fstBuy + p);
secBuy = Math.max(secBuy, fstSell - p);
secSell = Math.max(secSell, secBuy + p);
}
return secSell;
}
}本质上也是考察的是对于状态的分析变化,需要我们理清昨天和今天的状态关系
4.第四个股票问题(k次买卖)
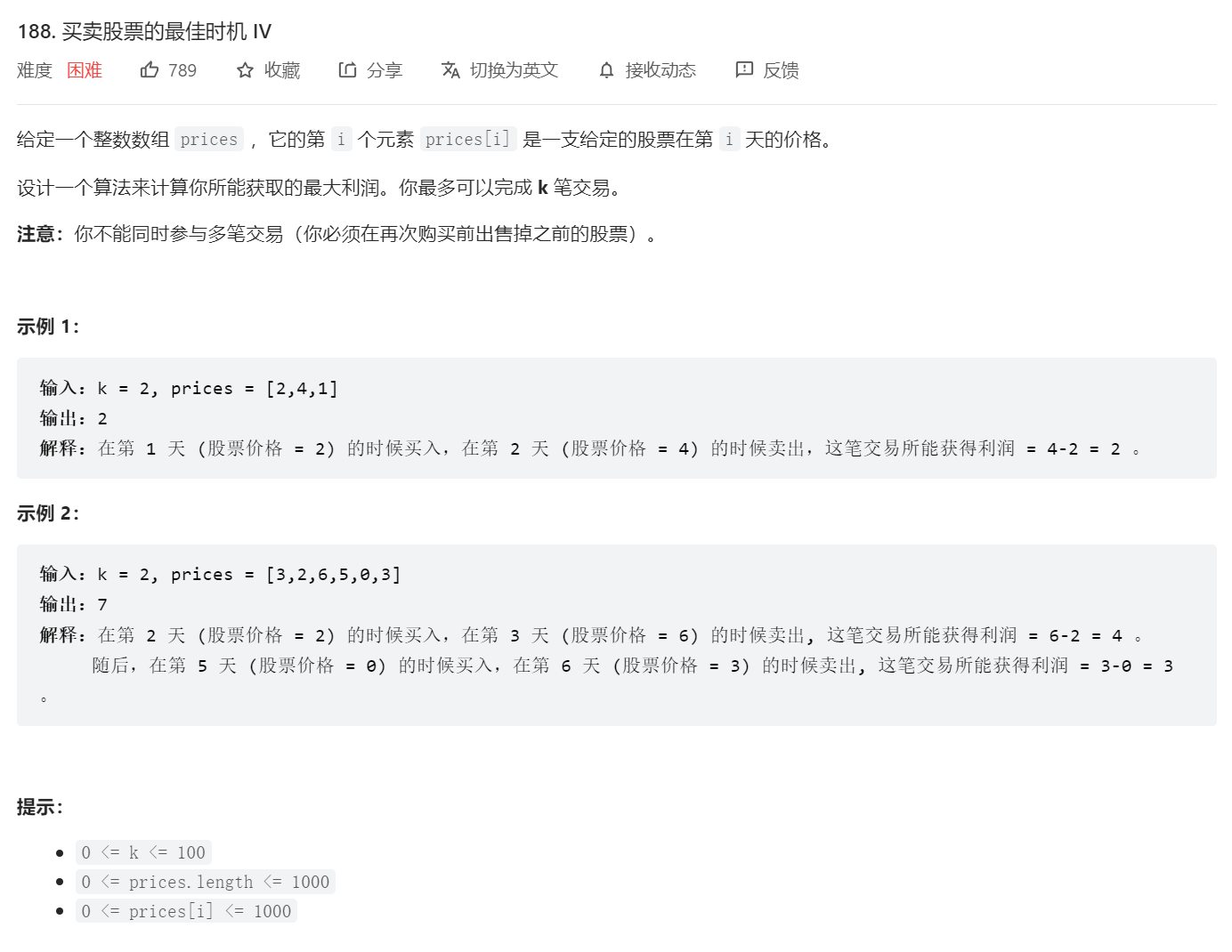
其实套路跟第三题一模一样,只是要求我们发现创建dp数组的规律
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public int maxProfit(int k, int[] prices) {
if (prices == null || prices.length <= 1) return 0;
int[][][] dp = new int[prices.length][2][k+1];
int MIN_VALUE = Integer.MIN_VALUE / 2;//因为最小值再减去1就是最大值,防止数据溢出
dp[0][0][0] = 0;//第一天休息
for(int i = 1;i<=k;i++){
dp[0][0][i] = dp[0][1][i] = MIN_VALUE;//不可能
dp[0][0][i] = dp[0][1][i] = MIN_VALUE;//不可能
}
dp[0][1][0] = -prices[0];//买股票
for (int i = 1; i < prices.length; i++) {
for(int j = 0;j<2;j++){
for(int l =0;l<=k;l++){
if(j==0&&l==0){
dp[i][j][l]=0;
}else if(j==1&&l==k){
dp[i][j][l]=MIN_VALUE;
}else if(j==0){
dp[i][j][l]=Math.max(dp[i-1][1][l-1]+prices[i],dp[i-1][0][l]);
}else if(j==1){
dp[i][j][l]=Math.max(dp[i-1][0][l]-prices[i],dp[i-1][1][l]);
}
}
}
}
int max = 0;
for(int i = 0;i<=k;i++){
max=Math.max(max,dp[prices.length-1][0][i]);
}
return max;
}
}
5.第二个股票问题加上冷冻期
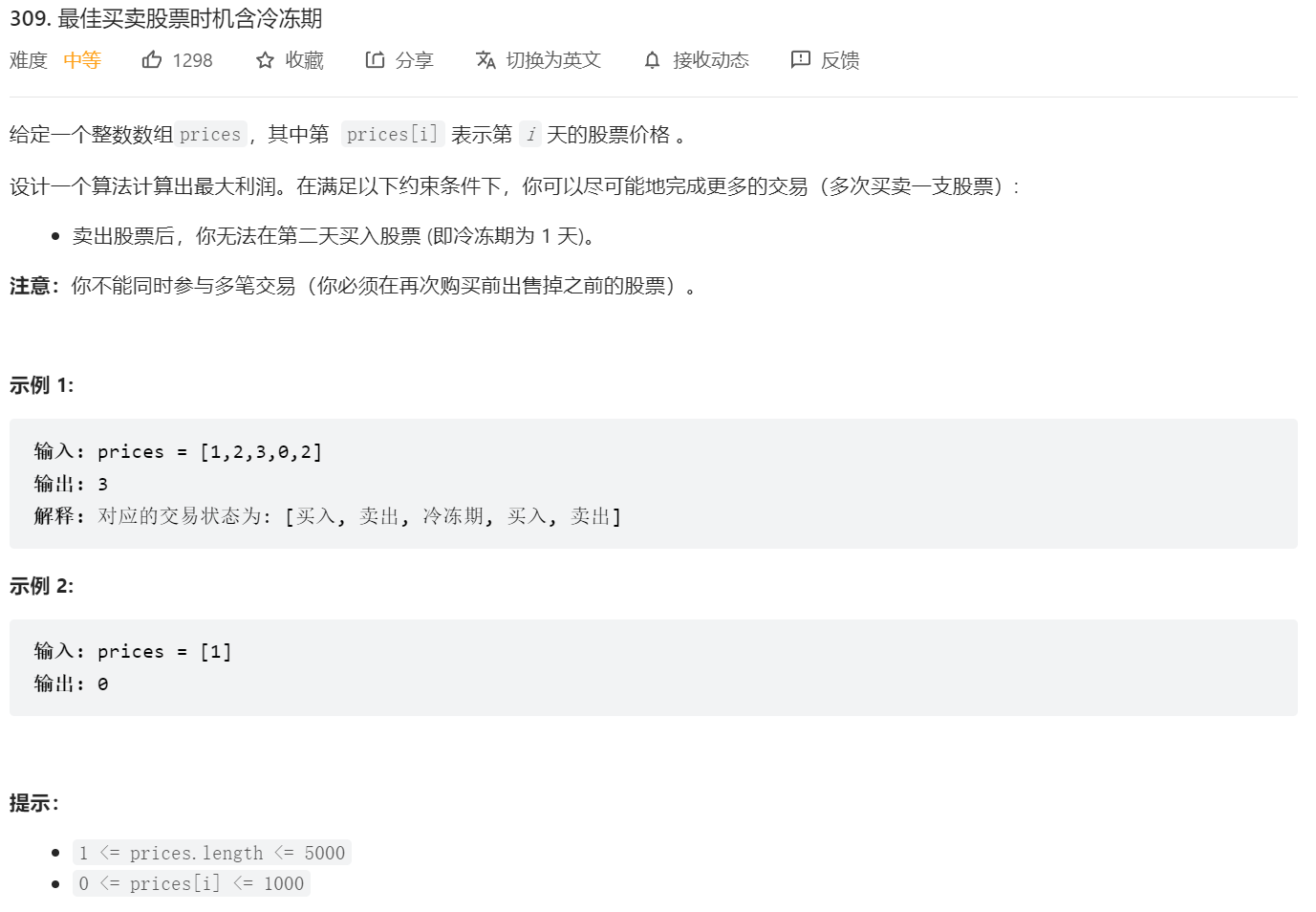
题目中定义的“冷冻期”=卖出的那一天的后一天,题目设置冷冻期的意思是,如果昨天卖出了,今天不可买入,那么关键在于哪一天卖出,只要在今天想买入的时候判断一下前一天是不是刚卖出,即可,所以关键的一天其实是卖出的那一天,而不是卖出的后一天
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int maxProfit(int[] prices) {
int n=prices.length;
if(n<=1) return 0;
//0代表不持股且当天没卖出
//1代表持股
//2代表不持股且当天卖出
int [][] dp=new int[n][3];
dp[0][0]=0;
dp[0][1]=-prices[0];
dp[0][2]=0;
for(int i=1;i<n;i++){//从[1]...[n-1]
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][2]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
dp[i][2]=dp[i-1][1]+prices[i];
}
return Math.max(dp[n-1][0],dp[n-1][2]);
}
}